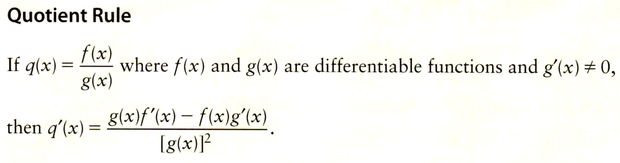Section 2.5: Derivatives of Quotients
Key Concepts:
You are expected to be able to differentiate simple quotient functions with and without using the Quotient Rule. To differentiate simple quotient functions without the Quotient Rule, you first have to rewrite the simple quotient functions as a product of two functions, one of which has a negative exponent (the denominator), then differentiate with both the Chain Rule and Product Rule.
You are expected to be able to differentiate simple quotient functions with and without using the Quotient Rule. To differentiate simple quotient functions without the Quotient Rule, you first have to rewrite the simple quotient functions as a product of two functions, one of which has a negative exponent (the denominator), then differentiate with both the Chain Rule and Product Rule.
Lessons for Section 2.5:
Derivatives of Quotients (Without Using the Quotient Rule)
Important: Don't forget to state any restrictions on the derivative functions!
Assigned Practices:
- eBook: Read p. 120 to 124
- eBook: Do exercises on p. 124 #3, #5 to 9
- eBook: In-Class exercises p. 118 #10 to 13, #15
|
|
|
3. Differentiate Using the Quotient Rule
Note: Make sure you bring the negative sign out.
It is ok to keep the denominator as a perfect product without expanding the brackets.
4. Quotient Rule Common Mistake Explained and Finding the Equation of a Tangent
It is ok to keep the denominator as a perfect product without expanding the brackets.
4. Quotient Rule Common Mistake Explained and Finding the Equation of a Tangent
5. Finding the Equation of a Tangent
Applying the Quotient Rule
1. Quotient Rule vs. Chain Rule
2. Chain Rule with Quotients (When to use the Quotient Rule with the Chain Rule)
|
|
|
Note: Make sure to reduce the derivative functions in rational form with the common factors.
3. General Power Rule with Quotient Rule (Example 1)
4. General Power Rule with Quotient Rule (Example 2)
5. A Quotient Rule Challenge
4. General Power Rule with Quotient Rule (Example 2)
5. A Quotient Rule Challenge
Assigned Practices:
- eBook: Read p. 128
- eBook: Do exercises on p. 129 #1 to 6
- eBook: In-Class exercises p. 129 #7 to 10