Section 2.1: Derivative of a Polynomial Function
Key Concepts:
Prior Knowledge:
- Recall answers to eBook exercises on p. 59 #9 to 13 (Check your notes)
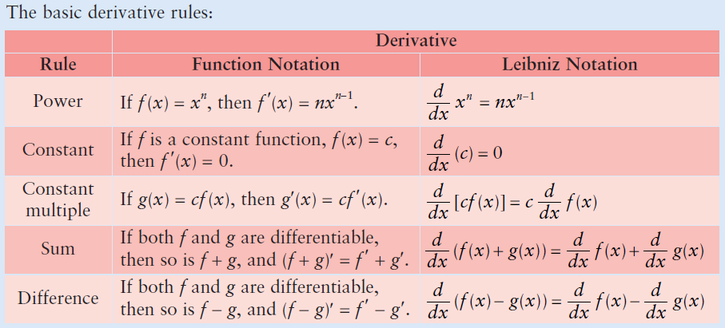
The Basic Derivative Rules: (Know them by heart!)
Lessons for Section 2.1:
Basic Derivative Rules
1. Constant Rule (Click on Explanation to view proof of the Constant Rule and check solution for Problem 1)
2. Proof and Application of the Power Rule
1. Constant Rule (Click on Explanation to view proof of the Constant Rule and check solution for Problem 1)
2. Proof and Application of the Power Rule
3. Proof and Application of the Constant Multiple Rule (with examples applying the Sum/Difference Rule)
|
|
|
4. Sum/Difference Rule (Click on Explanation to view proof of the Sum/Difference Rule)
Applications of Derivative Rules:
1. Applying the Power Rule (Finding derivatives of power functions in various forms e.g. rational exponents)
2. Finding the Equation of a Tangent Line Using the Power Rule
3. Derivatives of Polynomial Functions: Applying the Basic Derivative Rules (Example 1)
4. Derivatives of Polynomial Functions: Applying the Basic Derivative Rules (Example 2)
5. Derivatives of Polynomial Functions: Finding the Equation of a Tangent Line (Example)
6. Derivatives of Polynomial Functions: Finding the Tangent Points for a Given Slope (Example)
7. Application of Derivative Rules (Equation of a Tangent Line and Coordinates of Horizontal Tangent Line)
Note: Keep slopes and coordinates in fractional form, not in decimal form!
8. Problem Solving Using Derivative Rules
Note: - Velocity function is the derivative function of the displacement function.
- Acceleration function if the derivative function of the velocity function.
- Answers in these cases can be in decimal form.
- If you prefer the option to view the YouTube videos in full screen, click Part 1, Part 2, and Part 3.
Note: - Velocity function is the derivative function of the displacement function.
- Acceleration function if the derivative function of the velocity function.
- Answers in these cases can be in decimal form.
- If you prefer the option to view the YouTube videos in full screen, click Part 1, Part 2, and Part 3.
Derivative Applications to Revenue and Cost Functions:
1. Marginal Revenue and Marginal Cost (Explanation)
2. Marginal Revenue and Marginal Cost (Example 1)
3. Marginal Revenue and Marginal Cost (Example 2)
Assigned Practices:
- eBook: Read p. 76 to 83
- eBook: Do exercises on p. 83 #1 to 8, #10 to 13
- eBook: In-Class exercises p. 85 #14 to 17